https://arxiv.org/pdf/1712.09482
Related Works
Noisy Labelsについての全体的なものはこちらを参照。 📄2020-Survey-A Survey of Label-noise Representation Learning: Past, Present and Future
- データのラベルをきれいにする Data Cleaningでは、間違っていると思われるラベルを除去する。
- 未知の真のラベルを隠れ変数として扱い、それを得るための生成モデルを構築する。
- (この論文では)損失関数だけを変更して、ノイズが来てもうまく学習できるような損失関数を選ぶ。
- 01損失は、対称的なラベルノイズに強いらしい。
先行研究はBinary Classificationについてだったが、この論文ではMulti-class Classificationについて考える。
問題設定
- データはで、ラベルは。
- 識別器はである。
- 損失関数はである。
- 以下のような目標関数の最小化を目指すのが学習である。
Noiseの定義
各データが、i.i.d.で一定の確率で別のラベルに置き換わることによって、Noisy Labelな問題設定が起きる。ノイズの置き換えのやり方は、対称、非対称の二種類がある。前述のサーベイ参照。
。間違う率の合算はこのようにおく。Ground Truthのラベルはとする。
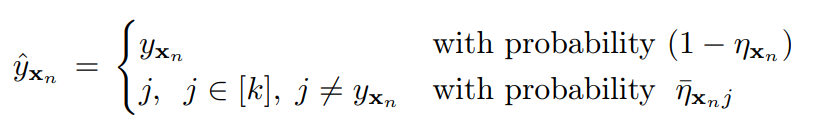
このフレームワークで、
- 対称な損失はとなる。
そして、ノイズがあるときの最適化というのは以下のようになる。
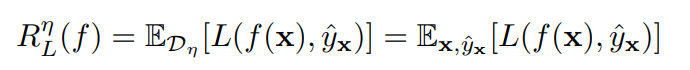
それぞれの全域最適学習器について、両方の学習器の予測を同じに入れて、それで識別をしてもらう(GANのDiscriminatorみたい)。それで、理論上完全な分離ができるのであれば、Noise Tolerantである。
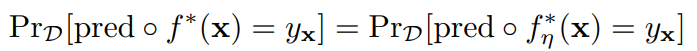
理論的な分析結果
まず、損失関数が対称的であるというのを以下のように定義する。
どのような識別器、データに対しても、予測されたすべてのクラスについての損失を足し合わせると、定数になる。
定理1
多クラス分類において、対称的な損失はであれば、対称的、一様的なラベルノイズに強い。
はラベルを間違えてしまう確率の合計。これが全クラス数に依存した以下、つまりほとんどの時である。
例として、Binary Classificationでは、5割以上間違えればどうがんばってもNoisy Labelの問題は解けないが、それ以下の間違え率ならば解ける。
証明
クリアなデータの時の損失は、である。
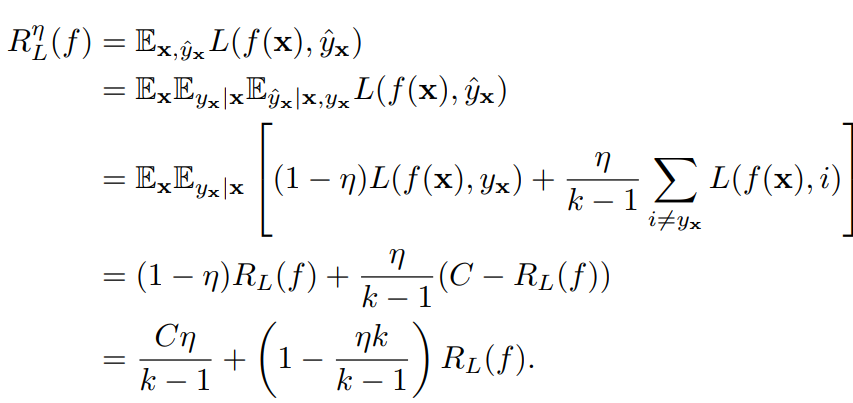
- 2行目は、条件付確率の分解をしている。として、ラベルをNoisyなものに置き換えている。
- 上のような分解では、右辺は結局となるが、ノイズラベルはサンプルの同時分布に従い生成するので、結局依存関係を持つを同時分布に組み込んだだけ。
- 3行目は対称ノイズの定義で展開している。
- 4行目は第一項は通常のについての期待値の積分で、これは通常の損失である。第二項は対称的な損失であれば、合算したから正解を引いたものに等しい。
- 対称的という条件は、間違ったときの損失の上界を抑えるためにある。
- 5行目は項をまとめると得られる。
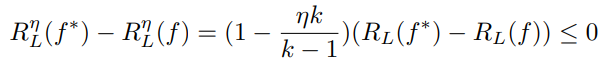
このを代入すると、
これは、Noisyなデータで学習したとき、あ
d
定理2
対称な損失関数について、識別器がを満たす=ちゃんとラベルに完全にフィットした学習ができる、のならば規則性のない損失関数であっても、である。
ただし、どうしてもになるなら、ノイズで学習したときの損失は0には収束せず、の上界を持つ。
はインスタンス依存のノイズ率であり、一律ではない規則性のない損失でも、同様に以下ならば対称な損失関数は強い。
定理3
対称な損失関数について、が成り立つとする。この時、と完全にフィットできるなら、が成り立つなら、ノイズに強いといえる。
意味は、クラス条件付きのノイズに対しても対称な損失関数は強いということ。
Neural Networkの損失関数
各種の損失について、具体的に書いてみる。CCEはクロスエントロピー損失、MAEは絶対値損失、MSEは二乗損失。
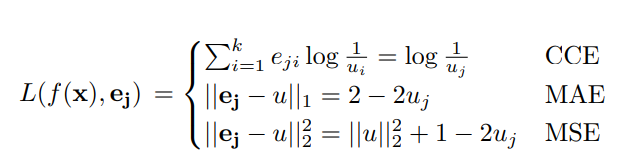
クロスエントロピー損失では実質1つのみのlogであり、それ以外でも似たように変形できる。
これについて、すべてのクラスにおいての総和を計算すると、
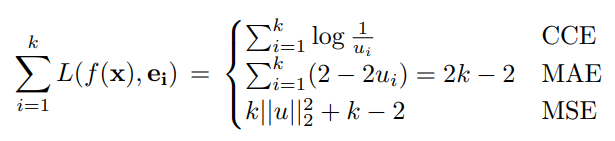
MAEだけが対称的な損失であるとわかる。他に、MSEも条件は満たしていないが、定理3のかたちのが成り立つので、これもこれで強い。
クロスエントロピー損失は損失に弱い。
